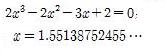INTRODUCE PRODUCT

수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.

Home
기업소개 수학사랑의 사업 제품소개 수학 소프트웨어 수학칼럼 수학사랑 소식 회원 서비스
회사소개 및 경영철학 연혁 오시는 길
수학문화사업 수학사랑 쇼핑몰 전시 프로그램 스페이스 해봄 열린학교 활짝
찾아가는 수학박물관 찾아가는 수학체험 교실 수학나눔 서초수학박물관 남양주 수학문화원
Exhibition
스케줄러
체험교구 전시교구 도서 과학수학정보 보드게임 메이커&공예 기타
인공지능 게이미피케이션 거꾸로코딩 GSP GrafEg Poly Tess Fathom Other S/W
거꾸로 코딩 소개 환경설정 관련자료실
인공지능 소개 관련자료실
게이미피케이션 소개 관련자료실
GSP 소개 GSP 평가판 다운로드 GSP 사용법 GSP를 활용한 수업 관련자료실 사진모음
GrafEq 소개 GrafEq 사용법 GrafEq 갤러리 관련 자료실
Poly 소개 Poly 다면체 Poly 포스터 관련 자료실
Tess 소개 Tess 사용법 변환군 기호 Tess 갤러리
Fathom 소개 관련자료실
여러가지 수학관련 소프트웨어
수학백과사전 송영준의 수학 따지기 송교식의 퍼즐 이야기 장훈의 횡설數설
회원 로그인 회원가입 아이디/비번 찾기 이용약관 개인정보취급방침

수학사랑 이야기

칼라비 삼각형

작성자 : 수학사랑|조회수 : 13477

정삼각형 안에 넓이가 최대가 되도록 내접하면서 합동인 정사각형 3개를 만들 수 있다.

이처럼 넓이가 최대가 되도록 내접하면서

서로 합동인 정사각형 3개가 되는 삼각형은 정삼각형 말고 한 가지가 더 있다.

칼라비 삼각형에서 가장 긴 변의 다른 두 변에 대한 길이의 비를 x 라 하면

이 수 x 는 다음 삼차방정식의 해이다.

              

(존 콘웨이, 리처드 가이, 이진주 역, 수의 바이블, 한승, 2003. 243-244 쪽)

이것을 증명해 봅시다.

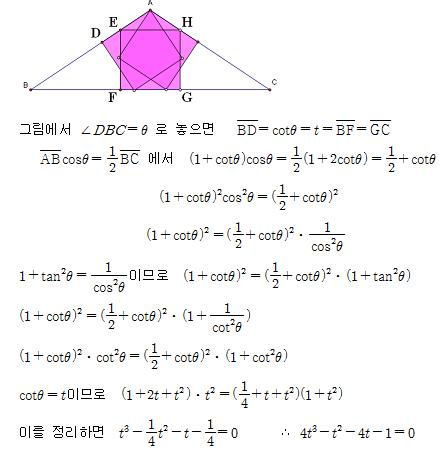
(풀이)

그림과 같이 내접하는 정사각형의 한 변의 길이가 1일 때,

 BD의 길이를 t라 할 때, t에 대한 방정식은 다음과 같이 구한다.

이제 이등변삼각형의 두 변의 길이의 비를 구하기 위하여

가장 긴 변의 다른 두 변에 대한 길이의 비 x 의  방정식을 구하여 보자.
목록
우편번호 검색 close