수학사랑

GrafEq 소개

GRAFEQ는 중고등학교는 물론 대학교 Calculus 과정의 모든 관계식(방정식과 부등식 포함)의 그래프를 쉽게 그릴 수 있는 프로그램이다. 즉, 다음 내용을 포함하고 있다.
일차함수, 다항함수, 이차함수, 삼각함수, 지수함수, 절대값을 포함하는 관계식, 기타

GRAFEQ에서의 수식 입력은 실질적으로 대부분 수학 프로그램에서 사용하는 표준 수식 표현 형식이다. 즉 타원을 그리려면 다음과 같이 입력하면 된다.
(x+1)^2/4^2 + (y-2)^2/3^2 = 1
입력된 식은 자동으로 다음과 같은 표준적인 수학 표현으로 바뀐다.

GRAFEQ는 주어진 관계식을 만족하지 않는 점을 제외하면서, 그 식을 만족하는 점을 남기는 지속적 정밀 좌표 찾기 작업을 통하여 그래프를 그리고, 남겨진 모든 픽셀이 관계식을 만족하면 그래프가 완성된 다. 이런 방법으로 음함수의 그래프 또는 부등식의 영역을 정확하게 표현할 뿐만 아니라 어떤 한 점도 제외되지 않는다. 이런 관계식은 다른 어떤 프로그램이나 그래핑 계산기로도 구현되지 않는다. 이 방법은 특이점의 좌표도 표현할 수 있게 한다. GRAFEQ는 수학 교사와 중등학생 및 대학생을 염두에 두고 개발되었다. 즉, 교실 수업을 위한 사용자 정의 상수, 사용자 정의 눈금, 줌 기능, 저장/열기, 인쇄 등이 모두 가능하다.

전형적인 프로그램의 사용에 대한 내용은 다음과 같다.

● 직선의 기울기와 절편 ● 다항함수 ● 변환 ● min/max ● 관계식의 연립과 교점

교사들은 다음과 같은 내용을 소개할 수 있다.

● 회전변환과 등적변형 ● 영역을 갖는 관계식 (x=|x|)

학생들은 다음과 같은 흥미있는 내용을 탐구할 수 있다.

● x 대신에을 |x|를 대입하면 그래프가 어떻게 바뀔까? ● 현수선과 포물선은 어떻게 다를까?

1. 기호판

기호판을 이용해 여러 가지의 관계식을 쉽고 편리하게 입력할 수 있다.
2. 수식의 표현

GRAFEQ는 기호판 또는 표준 수식 표현으로 관계식을 입력하면 즉각적으로 그 그래프를 그린다.
- ● 곱셈기호를 생략하여 입력한다. 즉 “2*x” 대신에 “2x”만 입력한다.
- ● 괄호 없이 입력할 수도 있다. 즉, “sin(2x)”대신에 “sin2x”를 입력해도 된다.
- ● 곱셈과 괄호에 대한 자동 번역이 가능하다.
  즉, “sin(x*y)cos(x)”대신에 “sinxycosx”를 입력가능
- ● sqrt, /, ^ , _ 등과 같은 표준 수학 표현을 근호, 나눗셈, 지수, 밑으로 인식한다.
  즉, “y=sqrt(x+1)”와 “(x-2)^2/3=(y-4)^2/3”를 입력하면 각각 다음과 같이 표현된다.
- ● xy의 절대값은 abs(xy)로 표현해도 되고, |xy|로 입력해도 된다.
- ● 구간에 따라 식이 다른 조건부 함수의 정의도 쉽게 입력할 수 있다.
  “y={x if x>0, 0 if x=0, -x if x<0}”
3. 일차함수의 그래프

일차함수의 많은 성질들을 GRAFEQ를 통하여 탐구할 수 있다.
예를 들어 GRAFEQ의 한 점 모드를 이용하여 직선의 x절편과 y절편의 근사값을 얻을 수 있다.
또한 두 점/기울기 모드에서 직선의 기울기의 근사값을 얻을 수 있다.
4. 다항함수의 그래프

어떤 다항함수라도 함수식을 수식 표현에 따라 입력하면 GRAFEQ는 그래프를 그린다.
5. 절대값 기호가 들어 있는 함수의 그래프
6. 천정함수와 마루함수의 그래프
- [x]는 x보다 크거나 같은 최소 정수를 뜻한다.
- [x]는 x 보다 작거나 같은 최대 정수를 뜻한다.
7. 이차곡선
8. 삼각함수의 그래프
- GRAFEQ에서 삼각함수 식을 입력하면 그래프를 그린다.
- 이 때 그래프 메뉴의 사용자 정의 눈금을 이용하면 좌표의 눈금을 정의할 수 있다.
9. 지수함수의 그래프
10. 로그함수의 그래프

기호판의 거듭제곱에서 역함수 부분을 누르면 지수함수로 되어 있던 부분이 로그함수로 바뀐다.
이것을 이용하여 로그함수식을 입력한다.
11. 문자의 값 지정

식에 들어 있는 문자의 값을 지정할 수 있다.
12. 부등식의 영역

어떤 부등식을 입력하면 GRAFEQ는 그 영역을 그린다.
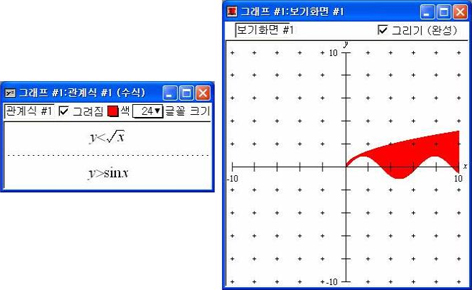
13. 연립부등식의 영역

여러 개의 부등식을 모두 만족하는 영역을 쉽게 그린다.