수학사랑

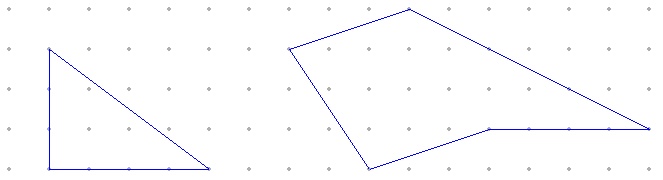
격자판 위에서 격자점을 꼭지점으로 갖는 단일 폐곡선인 다각형의 넓이S는 다음과 같다.

S = I + ½B - 1

이 때, I는 다각형의 내부의 점의 개수이고, B는 다각형의 경계에 있는 점의 개수이다.

예를 들면,

왼쪽 삼각형에서 내부의 점은 3개이고, 경계 위의 점은 8개 이므로 넓이는 다음과 같다.

S = 3 + ½ × 8 -1 = 6

실제로 밑변이 4, 높이가 3이므로 넓이가½ × 4 × 3 = 6 이다.

한편 오른쪽 오각형은 내부의 점이 13개, 경계 위의 점은 10개 이므로 넓이는 다음과 같다.

S = 13 + ½ × 10 - 1 = 17