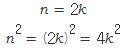|
대우/contraposition
작성자 : 수학사랑|조회수 : 32767 |
명제 p→q 에 대하여 ~q → ~p를 명제 p→q의 대우라고 한다. 명제 p→q와 그의 대우 ~q →~p는 서로 동치이다. p→q ≡ ~q →~p 따라서 명제p→q를 증명하기가 곤란할 때 그의 대우 ~q →~p을 증명해도 된다. 예를 들어 명제 " n²이 홀수이면 n도 홀수이다."를 대우인 " n이 짝수이면 n²도 짝수이다."를 이용하여 증명하면 된다.
(증명) n 을 짝수라고 하면 자연수 k에 대하여
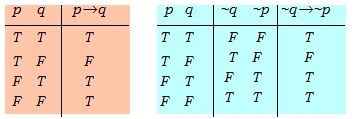
즉, n²은 짝수이다. (증명끝) 대우는 한자로 대할 대(對)와 짝 우(偶)로서 마주 대하고 있는 짝이란 뜻이다. 명제p→q와 그의 대우~q →~p가 서로 동치임은 다음 진리표로 증명한다.
|
MATH STORIES
수학백과사전에서 칼럼까지
수학사랑에서 알려드리는 수학과 관련한 이야기들